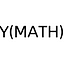Member-only story
The Pigeonhole Principle
A simple, common sense mathematical principle that allows us to prove some wonderful results.

The pigeonhole principle is one of the simplest and most intuitive principles in mathematics, while also being one of the most useful. Simply put, it states that if you place n balls (pigeons) inside of k boxes (pigeonholes), where n>k, then at least one box must contain more than one ball.
Also commonly referred to as Dirichlet’s box principle, due to Dirichlet’s treatment of the principle in the 19th century, the pigeonhole principle can answer some very straightforward questions, such as those given below, but similarly, it can be used to show some maybe not so obvious results, such as Dirichlet’s theorem, described below.
Let us look at three very simple applications of the pigeonhole principle.
Example 1
There are at least two people in Ireland with the exact same number of hairs on their heads.
This again is quite simple to see once you know 2 things:
1. The population of Ireland is more than 5 million.
2. The average person has around 150,000 hairs on their head.
So we can imagine the boxes (pigeonholes) as the number of hairs someone has, and the balls (pigeons) as the 5 million people. Then, since we have more balls than boxes, there must be at least two people in the same box, i.e. with the same number of hairs. We could actually go a step further and say that since 5,000,000/150,000=33.333… there are at least 33 people in Ireland with the same number of hairs on their head, although this is assuming 150,000 is the maximum number of hairs anyone has.
Example 2
Suppose that we have a bag containing 100 socks, 50 white, and 50 black. Now imagine we start blindly pulling out socks looking for a pair. What is the minimum number of socks we need to pull out in order to guarantee a pair?
Whenever I present this question to a class, quite often the answer I am given is 52. The logic behind this answer seems to be that if the first sock pulled is, for example, a black sock, then the worst-case scenario is that we pull 50 white socks in a row before getting the second black sock. This answer would be right if…